Paper presented at the 3rd Asian Technology Conference in Mathematics, Computer Technology in Mathematical Research and Teaching, August 24 - 28, 1998, University of Tsukuba, Japan
--
Iguchi, I., & Suzuki, K. (1998). Improving Junior-High Geometry by using a Drawing Software. In W.C. Tang, K. Shirayanagi, S.C. Chu, & G. Fitz-Gerald (Eds.), Proceedings of the Third Asian Technology Conference in Mathematics, August 24 - 28, 1998, Tsukuba, Japan, Springer-Verang, Singapore, 255-261.
Improving Junior-High Geometry by using Construction Software
Iwao IGUCHI & Katsuaki Suzuki
Graduate School of Human Informatics
Tohoku Gakuin University
Sendai, Japan, 981-31
Cabri Geometry, a French-made construction software, was used to redesign the 32-hour 9th grade geometry unit to motivate the students in engaged activities. Many practical and innovative research have shown affective effectiveness of the use of construction tools mainly in a short term. However, those effects may have only been because of novelty, that won't last long. In this study, the entire 9th grade's geometry unit was redesigned by incorporating Cabri in eight lessons, without exceeding regular length of the geometry unit. A comparative tryout of the geometry unit was conducted with one intact class (Cabri Group), whereas other classes continued regular teacher-led geometry lessons (Control Groups). Analyses using ARCS motivation design model of Cabri Group showed significant gains in Confidence aspect only, whereas decline in Confidence and Satisfaction aspects was found in Control Group. The final exam showed no significant differences of scores among classes, resulting no disadvantage in Cabri Group from introduction of and the time required to learn the construction software. Further study is needed to identify the effects of using construction software on higher order mathematical skills that were not tested in the regular final exams. Also needed is a refinement of the redesigned unit and then conduct of the unit by another teacher, so that this proposal can be a useful package for all teachers with construction software.
Keywords: Geometric Construction Software, Cabri, Junior-High Geometry, ARCS model
Introduction
Cabri Geometry, a French-made construction software, enables the users manipulate figures on a computer screen, measuring such properties as length of a line segment and angles. That is, geometry students can move figures easily to test hypotheses of figure's characteristics, finding dynamic properties and general properties inductively. Introduction of a construction software has affective impact as well, by making students actively and self-directively engaged in manipulation of figures. Recent improvement of technology enabled a construction software built into graph calculators, that makes easier utilization of the software with no computers in classrooms.
Many practical and innovative research have shown both cognitive and affective effectiveness of the use of construction tools. But those research have been conducted mainly in a short term. Those effects may have only been due to novelty, that won't last long. Although innovative uses of construction software should be sought to make future curriculum enriched, they may not fit into current curriculum where the use of such new tools were not taken into account.
When one desires to introduce a construction software into geometry lessons, training time is needed for the students to learn how to use the software. It has been pointed out that using a construction software may detract students attention to things that teacher has not planned in the lesson. All initial investment in time and distraction should be overcome by utilizing the software in a long run.
In this study, the entire 32-hour 9th grade's geometry unit was redesigned by incorporating Cabri in lessons and carried out by the first author, without altering learning objectives of the current curriculum, and without exceeding regular length of the geometry unit. Detailed lesson plans and teaching materials, as well as evaluation plans, were prepared prior to the tryout of the proposed unit, so as to make the proposal a package for other teachers after the tryout. It was expected that the use of Cabri would not have negative impact on cognitive student learning, but have positive impact on affective or motivational aspect.
Evaluating Affective Effectiveness: The ARCS Motivational Model
Keller (1992; Keller & Suzuki, 1988) has proposed a four factor model of learner motivation for designers and developers of instructional materials and lesson plans. It is called the ARCS motivational design model, that represents four factors of Attention (includes the novelty effect), Relevance, Confidence, and Satisfaction. It becomes possible by adopting the ARCS framework to determine which of the motivational factors may have an impact, both from existing geometry (or mathematics) curriculum, and from introducing new learning tools such as Cabri.
Prior to this study, Iguchi and Suzuki (1996) have developed a questionnaire using this ARCS framework to investigate why students of mathematics like or dislike math lessons. The questionnaire consists of 15 Semantic Differential Items on a 5 point Likert scale. This questionnaire and other constructive response items were used in this study, as a main indicator of affective changes in students, when new redesigned unit was carried out.
Redesigning Existing Geometry Unit
Analyzing Existing Geometry Units
Task analysis was conducted based on mathematics textbooks by 1996 Tokyo Shoseki for grades 7 through 9. A relational diagram was created depicting prerequisite relationships among contents of geometry lesson. It became clear that the 9th grade geometry unit was divided into 4 sub-units. For the first sub-unit of similarity and measurement, 8th grade's similarity and 7th grade's circles and arcs were prerequisites. Two review lessons were then planned to cover each of the two prerequisites at a time, while introducing various elements of Cabri, so that the students could get used to the software.
Cabri Lesson Design Principles
The regular 32-hour 9th grade's geometry unit was redesigned by locating Cabri lessons where seemed appropriate. Cabri was to be used in a total of eight lessons, including the two review lessons. In order to assist students' self-directed pursuits when using Cabri, a map of Cabri commands was created to show the English menu structure of Cabri in Japanese. When Cabri was used, the class moved to a computer lab, where one Macintosh was available to each of the students, although discussion and information exchange were encouraged when faced any problems.
Worksheets were prepared for each Cabri lessons, to help students record progresses, and to help the teacher monitor students' progresses. Basic items of the worksheets were decided to include: (1)Things I learned in this lesson, (2)Things I became able to do, (3)Things I would like to try, (4)Things I discovered, (5)Impression of this lesson (by 4 SD scales), and (6)Comments.
Sample Lessons with Cabri
Lessons with Cabri were designed so that the software was used according to the students' and contents' needs. Four types of Cabri lessons were as follows:
(1) Provide students with a basic figure already drawn by the teacher. Students were to move parts of the figure so as to find rules by themselves (Lessons 1, 2, 3, and 7).
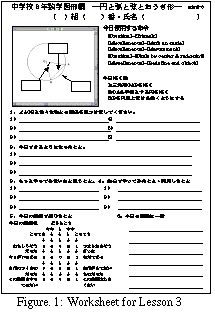
In lesson 3, for example, lesson objective was to be able to state relationship between inscribed angle and the length of the arc, the length of the chord, and the area of a sector. Students were given a worksheet (Figure. 1) and a basic figure on Cabri that was the same as the one on the worksheet. Students were then asked to manipulate Cabri commands so that the length of arc, etc. and the angles were measured. Free exploration time followed when the students tried to find any interrelationships among the parts' measurement by moving points.
(2) Lecture basic principles first, then let the students verify what was lectured using Cabri. Students were to explore if the principles really applies and when (Lessons 10, and 14).
Lesson 9 was to lecture relationships among similitude ratio, the curcumference, and the area of the figure, in the case of a triangle as an example. Lesson 10 then expanded the case up to Octagons by providing two similar Octagons as shown in Figure 2. There were hidden relationships set from the leftmost indicator of similitude ratio to two Octagons so that any movements of any points in three figures will move related figures so that similar relation of the two Octagons would be maintained. By moving a point on the top of another point in the same Octagon, the figure could be made simpler, down to a triangle.

Students were to manipulate this given figure to examine if the relationships that were taught in lesson 9 could be the case, not only in triangles but in other polygons. Worksheets were provided to record the figures students made and the measurements they had, and whether or not the relationships were hold true.
(3) Provide students with a blank sheet on Cabri to create by imitating the figures they saw in the textbook. Students were expected to use Cabri commands freely to specify the relationships among parts of the figure (Lesson 21).
In lesson 21, when the students were used to Cabri commands, they were asked to choose among figures in the textbook, and to create the same figure on Cabri from scratch. Figure 3 shows one of students work on Cabri screen and on a worksheet with comments. Some students imitated the outlook of figure without capturing the relationships among parts, so that when a part of the figure was moved, the relationship did not hold constant. This showed how much the students understood the relationships represented in the textbook's figure.

(4) Provide students with a new figure on Cabri to anticipate and discuss relationships among the parts, before manipulating the figure (Lesson 26).
Prior to lesson 26, three problems were given to the students (Figure 4). They tried to answer to the problems before the lesson, then to verify their anticipations with Cabri in the lesson. In the following lessons, geometric proof was demonstrated by the teacher for the three problems.
Method of the Tryout
Participants
A comparative tryout of the redesigned geometry unit was conducted at an urban boys' private junior high school. One intact class of the 9th grade was taught under redesigned unit using Cabri (Cabri Group), whereas other 3 classes continued regular teacher-led geometry lessons (Control Groups). Cabri Group consisted of 46 boys, and Control Groups a total of 138 boys, within which 41 and 116 boys who had all the data available, respectively, were analyzed. The geometry unit was taught during the entire first semester (20 hours) and the first part of the second semester (12 hours) with a 1 1/2 month summer break in between.
Measures
In all of the four classes, pre- and post-questionnaire were conducted using the ARCS framework (Iguchi & Suzuki, 1996). Also administered were term-beginning, midterm, and final examination for the first semester, and the midterm examination for the second semester, all related to geometry. Within the Cabri Group, all the lessons were video-taped for a record, and in all Cabri lessons worksheets were collected, photocopied, and returned to monitor students progresses and to give feedback to students.
Results and Discussion
The average standard scores for each class on examination were shown in Figure 5, with Cabri Group as Class D, and Control Groups as Class A , B, and C. An analysis of co-variance on the 1st semester's midterm, final, and 2nd semester's midterm scores with term-beginning exam scores as a covariate showed no significant differences among classes (F(3,178) = 2.05, F(3, 176) = 1.30, and F(3,173) = 1.26, respectively, p> 0.05). Although the class average was the lowest in Cabri Group, no disadvantage in Cabri Group was shown from introduction of and the time required to learn the construction software.
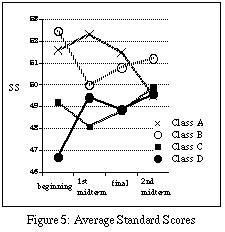
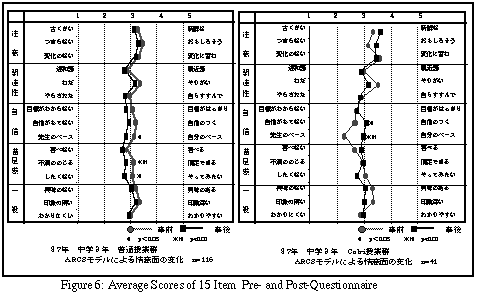
Figure 6 shows the average scores of 15 items on pre- and post-questionnaire from Cabri and Control Groups. The average scores of Control Group declined in most of the items. Paired T-test revealed there were statistically significant decline in three items: teacher's pace vs. my own pace item (t(115) = -2.61, p< 0.05), unsatisfied vs. satisfied item (t(115) = -3.08, p< 0.01), and unwilling to continue vs. willing to continue item (t(115) = -2.47, p< 0.05). On the other hand, Cabri Group showed positive shift in most of the items. Paired T-test indicated significant gains in two Confidence items only: feel unconfident vs. feel confident item (t(41) = 2.16, p< 0.05), and teacher's pace vs. my own pace item (t(115) = 4.25, p< 0.01).
The tryout of the redesigned unit of 9th grade geometry with Cabri showed that such a revision of the existing curriculum can be feasible and as effective as regular teacher-led instruction. This means that a construction software may be introduced to junior-high geometry without interfering current curriculum, spending as many class hours as the regular classes. The time required for the students to master Cabri commands needed for the learning can be absorbed within the allocated time, if the tool was used repeatedly throughout the unit. Further study is needed to identify the effects of using construction software on higher order mathematical skills that were not tested in the regular examinations.
By administering pre- and post-questionnaire based on the ARCS model, it was found that not the novelty effects (Attention in ARCS model), but Confidence was what was gained from the use of Cabri for a long period of time. Further analyses were needed to determine what aspects of the Cabri lessons caused such a gain in Confidence factor. Lesson records would be beneficial to carry out detailed analyses of redesigned lessons.
Also needed is a refinement of the redesigned unit and then conduct of the unit by another teacher, so that this proposal can be a useful package for all teachers with construction software. A package would include such items as teachers guides, worksheet templates, lesson plans, evaluation plans with questionnaires, so as to disseminate ideas to utilize construction software in schools.
References
Iguchi, I. & Suzuki, K. (1996). Research on improving junior-high school geometry. Proceedings of the 12th Annual Conference of Japan Society for Educational Technology, 361 - 362 [In Japanese].
Keller, J. M. (1992). Enhancing the motivation to learn: Origins and applications of the ARCS model. Reports from the Institute for Educational Research, 11, 45-67, Tohoku Gakuin University, Sendai, Japan.
Keller, J. M., & Suzuki, K. (1988). Use of the ARCS motivation model in courseware design. In D. H. Jonassen (Ed.), Instructional designs for microcomputer courseware. Lawrence Erlbaum Associates, USA, Chapter 16.





