十進法と二進法

数字を書けるようになった子どもの時のことを思いだしてみましょう。 三個物があると、何の疑いもなく「3」と書き、5個あると「5」と書きました。 ところが、十個物があると「じゅう」と呼ぶ(数える)ことはできましたが、 自然に「10」と書くことができたでしょうか？

我々は、通常０?９までの十種類の文字(いわゆる数字)だけで数を表現します。 この節では、どのようにして十種類の文字(数字)だけで、 十以上の数を表現するか(しているか)について良く考えてみましょう。

この節では、数を表わす文字(数字)は、０～９までの十種類しか無いとします。 (そのような世界に住んでいると考えて下さい。)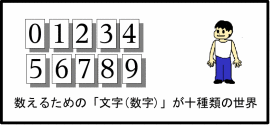

以下のように９までは、問題なく数を表現できます。

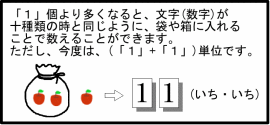
ところが、文字(数字)は、十種類しかありませんので、９を超えると、 表現すべき文字が無くなってしまいます。

(例えば「十(じゅう)」のように)９+１を表わす文字(数字)を作れば良いのですが、 十種類の文字(数字)で表現することにしていますので、 それ以外の文字を使うのはルール違反です。

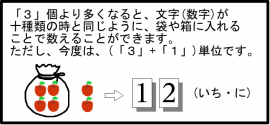
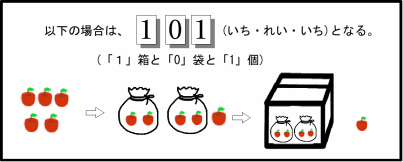
そこで、９より１大きい数(これは、利用できる文字の数と同じです)を一塊(ひとかたまり)として 「１０」(「いち・れい」と読む)と、 表わすことにします。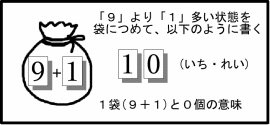
(注意) 「じゅう」ではなく、必ず「いち・れい」と読んで下さい。

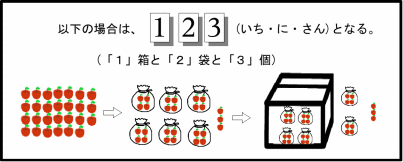
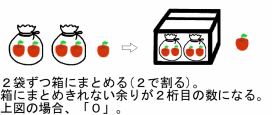
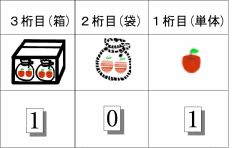
この「１０」は、９より１大きい数を表わす塊が１つで、 ０から９までの数を表わすことのできる部分が ０(何もない)と解釈することができます。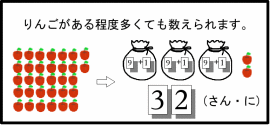
すると、「１０」が２つあれば「２０」と書くことができますし、 「１０」が３つと単体(図ではリンゴ)が２あれば「３２」と書くことができます。 (図では、３袋と２個ですね。)

更に「１０」の数 (図の袋の数)が９より多くなったら、 「１０」が「１０」個あることを表わす「１００」(「いち・れい・れい」とよむ) を導入することで(図では箱で表わしている)、 それ以上の数も数えられるようになります。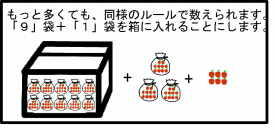

このように、０から９までの十種類の文字(数字)で、 数を数える方法を「十進法」と呼びます。
また、文字の種類の数(より正確には、１桁で表わすことできる数の種類)を 「基数」と呼びます。

我々の生活では、十進数を用いることが多いので、十進数には、 各桁(塊)に名前がついています。先の図でいうと、「袋」は「十(じゅう)」と、 「箱」は「百(ひゃく)」と呼ばれます(知っての通りです)。 ですから、十進の世界で表現した「１(箱)３(袋)６(個)」は、 「百三十六」と呼びます。

それでは、もし、０?３までの四種類の文字(数字)しかない世界では、 どのように数を数えるのでしょうか？

０から９までの十種類の数字がある世界(十進法)と同じ考え方で、 数えることができます。(四進法)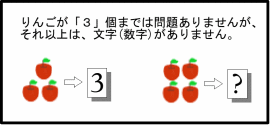
   (ただし、基数が４ですので、袋や箱が小さいですよ。)

同様にして、０と１の二種類の文字(数字)しかない世界でも、 数を数えることができます。

ただし、基数が二ですので、袋や箱はもっと小さいですよ。(二進法)

時間で使う十二進法、六十進法

時間は、十二進法や六十進法が使われますね。ただし、この場合、 数字は通常の十進法の０から９までが使われますので、少し複雑ですね。

例えば、59分+1分が1時間となり、分を１桁で表わせなくなってます。 もし、0から59までをすべて１文字(１桁)で表現できたら、時間の計算は、 もっとスッキリするでしょうね。

PCの世界では、十六進法が使われる場合があります。
何進法でも考え方は同じなのですが、十六進法は、 十二進法や六十進と異なり、十六種類の文字を使って表わします。

０から９までは、通常の数字を使い、それ以上は、ａからｆを用います。 十進の「10」が十六進では「a」と表わされ、 十進の「14」が十六進では「e」と表わされます。

累乗(るいじょう)というのは、 ある一つの数同士を繰り返し掛け合わせるということ、 あるいはそれによって得られる数のことです。

Ａⁿ は、Ａを n 回掛け合わせものと定義し、 これを Ａの n 乗(じょう)と呼びます。
例えば、７⁴ は、 ７を４回掛け合わせた ７×７×７×７ を表わし、 ７の４乗と呼びます。

Ａ² は、Ａ × Ａ を表わしますが、 Ａ¹ (Ａの１乗) は、Ａ そのものを表わしています。

それでは、Ａ⁰ (Ａの０乗) は、何を表わすでしょう？ これは、１(いち) になります。Ａが０を除くどんな数(正確には実数)であっても、 必ず １ になります。これは、そのように定義してあると思ってもらっても結構です。 もう一度書きますが、 Ａの値に関係なく(Ａ=０は除く)、 Ａ⁰ ＝ １ です。

N進法の世界で生きている人が、そのN進法のみで生活できるなら、 何の問題もないのですが、お互いの変換が必要になることがあります。

我々は、十進の生活に慣れていますので、 PCの得意な二進法や十六進法で表わされた数は、ピンときませんし、 逆に、我々の考え得ている十進法の数を、 二進法や十六進法で表わさなければならないことがあります。

ここで、これまでは、N進法しか扱わないそれぞれの世界での中だけで、 考えていましたので問題は無かったのですが、 複数の基数の数を同時にあつかうとなると注意が必要です。 単に「101」と書くと、十進の「101」(いわゆる「百一」)なのか、 「二進」の「101」(十進で表わすと「五」)なのか区別がつきません。

そこで、今後は、基数を右下に括弧で書くことにします。 例えば、十進の「101」は「101_(十)」と、 二進の「101」は「101_(二)」と表わすようにします。 また、何も書いてなかったら十進法の記述だと解釈して下さい。

先に二進法の説明で使った下図を例にして、その変換方法を考えてみましょう。

◎ 十進法で表わされた数を、二進法で表わすには、 以下のようにすれば良いことが分ります。
     (上図の矢印方向の変換です。)

1. まず、基数(袋)でまとめた(割り算した)余りを求めます。 すると１桁め(リンゴ単体)の数がわかります。





2. 次に、基数(袋)でまとめたものを、更に基数個(箱)でまとめます。 このときの余りが、２桁目(余った袋)の数です。 (上図では、余った袋はありませんね。)





3. 以下同様に、基数毎にまとめて余りを求めていくと、 下位の桁から順に求めることができます。
4. まとめるものが無くなったら(商が０になったら)変換は終りで、 そのときの余りが、最上位の桁になります。

(例 １)
具体的な例として、
「 十進法で表わされた ４３４ (四百三十四) を、 二進法で表わす 」
ことを考えます。
十進法で表わされた数を、Ｎ進法で表記するには、 上の説明のように、 十進表記された数をＮで割りその余り順に求めて行けば良いので、 以下のように計算できます。ただし、ここでは、二進法で表わすので、 Ｎ＝２ となります。(２で繰り返し割って行きます。)
      2)434
      2)217　…　0    (２進表記の最下位)
      2)108　…　1    (２進表記の下位から２桁目)
      2) 54　…　0    (２進表記の下位から３桁目)
      2) 27　…　0    (２進表記の下位から４桁目)
      2) 13　…　1    (２進表記の下位から５桁目)
      2)  6　…　1    (２進表記の下位から６桁目)
      2)  3　…　0    (２進表記の下位から７桁目)
      2)  1　…　1    (２進表記の下位から８桁目)
          0　…　1    (２進表記の最上位(９桁目)) 
ですから、十進法で表わされた ４３４ (四百三十四) を 二進法で表わすと、
「１１０１１００１０」
となります。

◎ 二進法で表わされた数を、十進法で表わすには、 以下のようにすれば良いことが分ります。
     (上図の矢印と逆方向の変換です。)

• 二進法で表わされたそれぞれの桁の数は、下位から順に、 以下の重みがあります。
1. 基数二の零乗 (一)(何にも入らないリンゴの個数)
2. 基数二の一乗 (二 (１袋の中のリンゴの個数))
3. 基数二の二乗 (四 (１箱の中のリンゴの個数))
4. 基数二の三乗 (八)
5. ...
• ですから、 二進法で表わされたB _(二) (= ...B₃ B₂ B₁ B₀ )を、 十進法のD _(十)に変換するのは簡単で、
  

  D _(十) ＝ ... +  B₃×２³  +  B₂×２²  +  B₁×２¹  +  B₀×２⁰

  のようにすれば変換できます。
  
  上の図のでは、B _(二)＝１０１ですので、 それを十進法で表示した D _(十)は、

  D _(十) ＝  １×２²  +  ０×２¹  +  １×２⁰ ＝ ４ + ０ + １ ＝ ５

  のように求めることができます。

(例 ２)
具体的な例として、(例 １)の結果を使い、
「 二進法で表わされた １１０１１００１０ を、 十進法で表わす 」
ことを考えてみましょう。
N進法で表わされた数を、十進法で表記するには、 上の説明のように、 各桁の重みを十進表記し、それぞれの桁をその重みに掛け合わせ、 すべてを可算すれば良いので、以下のように計算できます。 ただし、ここでは、二進法で表わされた数を十進で表わすので、 下位から ｎ 桁めの重みは、２^n-1 となります。
  １×２⁸ + １×２⁷ + ０×２⁶ + １×２⁵ + １×２⁴ + ０×２³ + ０×２² + １×２¹ + ０×２⁰
＝ ２５６ + １２８ + ０ + ３２ + １６ + ０ + ０ + ２+ ０
＝ ４３４
ですから、二進法で表わされた １１０１１００１０ を、 十進法で表わすと、
「４３４」
となります。これで、 (例 １)で、十進法で表わしたものに戻ることがわかります。

(回答例)

       
    054-T3298   総情 先太

1. 98 (十)  ==>   1101110 (二) 

(ただし、上の回答例の計算は、わざと間違っていますので、 ９８ の人もちゃんと計算して下さい。)